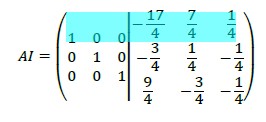
特異値分解(SVD)について、分かりません。
だれかコメントで教えてほしいです。
一応、以下の方法だと解ける。
・特異値分解とは…主成分分析 (PCA)と並ぶ次元削減手法。すべての実行列を
特異ベクトルと特異値に分解する。単語の出現頻度解析や
画像処理や自然言語処理に用いられる。
$ A= \begin{pmatrix}3 & 2 & 1 \\1 & 2 & 3\end{pmatrix}$を$A=UDV^\mathsf{T} $となるように特異値分解したい。
$AA^\mathsf{T}=\begin{pmatrix}14 & 10 \\10 & 14 \end{pmatrix}$の固有値を計算すると、大きい順に$λ_{1}=$(あ)、$λ_{2}=$=4となり、それぞれに対応する固有ベクトルが求まる。そのため、Aの左特異ベクトルとして$U=\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & (い) \end{pmatrix}$を求めることができて、同様に$AA^\mathsf{T}=\begin{pmatrix}10 & 8 & 6 \\ 8 & 8 & 8 \\ 6 & 8 & 10 \end{pmatrix}$の固有ベクトルを求めることで右特異ベクトルVを求めることができる。その結果、特異値分解の結果のうちの一つとして$A=\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & (い) \end{pmatrix}\begin{pmatrix}(う) & 0 & 0 \\0 & 2 & 0\end{pmatrix}\begin{pmatrix} \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{-1}{\sqrt{2}} \\ \frac{1}{\sqrt{5}} & (え) & (お) \end{pmatrix}$を得ることができる。
・ (あ)…固有値
$AA^\mathsf{T}=\begin{pmatrix}14 & 10 \\10 & 14 \end{pmatrix}$対角線にλで引く。固有値 𝜆𝜆=24,4 ルートしたものが特異値σ= 2√6,2 つまり (う) = 2√6(あ)=24